Fibonacci Serisi ve Altın Oran

FİBONACCİ DİZİSİ NEDİR: Fibonacci dizisi, 0 ve 1 ile başlayan ve her sayının kendisinden önce gelen iki sayının toplanması ile elde edildiği bir sayı dizisidir. İtalyan matematikçi Leonardo Fibonacci‘den adını alır.

Fibonacci Sayıları

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

Bazı kaynaklarda fibonacci sayıları 0’dan değil 1’den başlatılır.

FİBONACCİ DİZİSİ KURALI

Fibonacci sayı dizisinin kuralını matematiksel olarak ifade etmede n’inci Fibonacci sayısını F(n) olarak gösterelim. Buna göre fibonacci sayı dizisi genel terimi şu şekilde yazılır:

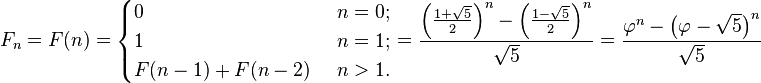
FİBONACCİ SAYILARI VE ALTIN ORAN

Fibonacci sayılarının ilginç özellikleri vardır. Mesela n sayısı büyüdükçe iki ardışık Fibonacci sayısının oranı Altın oran’a yani 1.618… e yakınsar.

İdeal güzelliğin matematiği olarak karşımıza çıkan altın oran 1205 yılında İtalyan Matematikçi Leonardo Fibonacci “Liber Abaci” adlı kitabında tavşan problemi ile oluşan bir sabiti “Golden Ratio” olarak tanımlamıştır. Genel anlamda ilk tanım bu kitapta veriliyor olsa da M.Ö 3000’li yıllara kadar yapılmış yapılarda bu oranı görmek mümkün. Fibonacci serilerinin tanımı ile başlayalım.

Fibonacci dizisi, her sayının kendinden öncekiyle toplanması sonucu oluşan bir sayı dizisidir. Bu şekilde devam eden bu dizide sayılar birbirleriyle oranlandığında altın oran ortaya çıkar, yani bir sayı kendisinden önceki sayıya bölündüğünde altın orana gittikçe yaklaşan bir dizi elde edilir. Fibonacci sayı dizisindeki sayıların birbirleriyle oranı olan ve altın oran denilen 1,618 sayısı ise doğada, sanatta ve hayatın her alanında görülen ve estetik ile bağdaştırılan bir sayıdır. Ayrıca Pascal Üçgeninde de fibonacci sayı dizisi bulunmaktadır.

Altın oran, matematik ve sanatta, bir bütünün parçaları arasında gözlemlenen, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Eski Mısırlılar ve Yunanlar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987.. dizisi Fibonacci sayı dizisi olarak geçiyor. Fibonacci sayı dizisinin özelliği kendinden önceki iki ardışık sayının toplamının kendisinden sonraki sayıya eşit olmasıdır. Yani her sayı kendisinden önce gelen iki sayının toplamıdır.

Tanım: Fn olarak gösterilen bir dizide her terim kendinden önceki iki terimin toplamı ile oluşan dizilere Fibonacci dizisi denir. Bu dizide ilk iki terim F1=1 ve F2=1 olmak üzere iki sabit üzerine kurulmuştur.

Dizinin terimleri: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …

Fibonacci bu serinin her bir terimini evinde beslediği tavşanların çoğalmasına göre oluşturmuştur. Aldığı tavşanlar aylara göre ilk başta anlamsız bir şekilde çoğalıyor gibi görünmesine rağmen aslında arkasında esrarengiz bir matematik vardı.

Bu oluşan serinin terimlerinin birbirine oranı belirli bir müddet sonra (limiti) 1.618 sayısına yakınsıyordu. İlk başta anlam veremeyen Fibonacci bu sayının alınan herhangi bir doğrunun keyfi bir noktasından alınan sabitin oranlarıyla ilişkili olduğunu gözlemledi.

İşte bu noktada bu sayının hiç de hafife alınacak bir sayı olmadığı gözlemlenmiş oldu. Fibonacci bu eşitliğin 1.618 sayısına denk gelmesinden sonra “İlahi Oran” olarak tanımlamış daha sonraları bu sabitin en önemli savunucusu Leonardo Da Vinci “İlahi Oranın Yansımaları” adı altında birçok eser ortaya çıkarmıştır. 17. yüzyılda ise biraz daha matematik kokusu barındıran bir diskriminant köklerine sahip denklemin çözümleri tanımlandı ve bu çözümlerin altın oran sabitine eşit olduğu görüldü.

Yunan Alfabesinin 16. harfi olan phi harfi ile gösterilmektedir. Bugün kullanılan antik eserlerin birçoğunda, sanatçıların sanat eserlerinde bu matematiksel güzelliği görmekteyiz.

Fibonacci daha sonra bu dizedeki sayıları bir dikdörtgenin içine yerleştirmiş ve sarmal biçiminde alanlarına göre büyüdüğünü farketmiş bunu ise etrafındaki salyangoz kabuklarının tıpkı aynısı gibi olduğunu keşfetmiştir. “Altın Oran Spirali” olarak matematik tarihine geçen bu sarmal matematikçilerin güzellik olgusunu bir anda değiştirmiştir.

Bu spiral altın oran bahsedildiğinde aklımıza gelmesi gereken yapıdır. Yukarıda sözü edilen doğru parçasının bir dikdörtgen biçimine getirilmiş halidir. Uzun kenarı a+b, kısa kenarı ise a olan bir dikdörtgenin içerisindeki sarmal sadece Fibonacci dizisine göre yerleştirilebilir. Sizlerinde göreceği üzere uzun kenarın kısa kenara oranı burada 1.618 olacaktır.

Bir dik üçgende e sayısı ile phi sayısı Pisagor teoreminin yardımı ile pi sayısının karesi ile yakından ilişkilidir. Bu matematiksel bağıntı matematik felsefesinin önemli sorularından bir tanesi olan “Matematik bir buluş mu yoksa icat mı?” sorusuna bir nebze cevap vermektedir.

Matematiksel olarak phi sayısının açılımı sürekli kesirlerle de ilgilidir. Sürekli kesirlerin girdileri 1,1,1,1,… olarak alındığında bu sayı direkt olarak altın oran olarak bilinen 1.618 sayısına yakınsamaktadır. Matematikçilere göre ideal güzelliğin matematiği olarak tasvir edilse de bu siz değerli okuyucuların insiyatifine kalmıştır.

Fibonacci Dizisinin Görüldüğü ve Kullanıldığı Yerler

Mısır’daki piramitler , Leonardo da Vinci’nin Mona Lisa tablosu, ay çiçeği, salyangoz, çam kozalağı ve parmaklarımız, yüzümüz hatta tüm bedenimiz bu sayı dizisine / altın orana sahip.Daha basit anlatımıyla altın oran; bütünün, parçaları arasında olan geometrik ve sayısal bir oran bağlantısıdır.

Ayçiçeği: Ayçiçeği’nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru taneler sayıldığında çıkan sayılar Fibonacci Dizisinin ardışık terimleridir.

Kollar: Kolumuzun üst bölümünün alt bölüme oranı altın oranı verir.

Mısır Piramitleri: Her bir piramitin tabanının yüksekliğine oranı altın oranı veriyor.

Ömer Hayyam veya Pascal veya Binom Üçgeni: Ömer Hayyam üçgenindeki tüm katsayılar veya terimler yazılıp çapraz toplamları alındığında Fibonacci Dizisi ortaya çıkar.

Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu taneler soldan sağa ve sağdan sola sayıldığında çıkan sayılar, Fibonacci Dizisi’nin ardışık terimleridir.

Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir Fibonacci Dizisi mevcuttur.

Fibonacci Dizisinin Fark Dizisi: Fibonacci Dizisindeki ardışık terimlerin farkıyla oluşan dizi de Fibonacci Dizisidir.

Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir Fibonacci Dizisi söz konusudur; yani yaprakların diziliminde bu dizi mevcuttur. Bundan dolayı tütün bitkisi Güneş’ten en iyi şekilde güneş ışığı ve havadan en iyi şekilde Karbondioksit alarak Fotosentez’i mükemmel bir şekilde gerçekleştirir.

İnsan Yüzü: Kulaklar arasındaki mesafe, gözle üst dudak arasındaki, burnun altı ile çene arasındaki mesafe altın oran içermektedir.

Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu’nda da vardır.

Mimar Sinan: Mimar Sinan’ın da bir çok eserinde Fibonacci Dizisi görülmektedir. Mesela Süleymaniye ve Selimiye Camileri’nin minarelerinde bu dizi mevcuttur.

Altın oran, matematik ve sanatta, bir bütünün parçaları arasında gözlemlenen, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Eski Mısırlılar ve Yunanlar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır.

lk olarak kimler tarafından keşfedildiği bilinmese de, Mısırlılar’ın ve Yunanlılar’ın bu konu üzerinde yapmış oldukları bazı çalışmalar olduğu görülmektedir. Öklid, milattan önce 300′lü yıllarda yazdığı “elementler” adlı tezinde “ekstrem ve önemli oranda bölmek” olarak altın oranı ifade etmiştir. Mısırlıların Keops Piramidinde, Leonardo da Vinci’nin “İlahi Oran” adlı çalışmada sunduğu resimlerde kullanıldığı bilinen “altın oran” , “Fibonacci Sayıları” olarak da bilinmektedir.

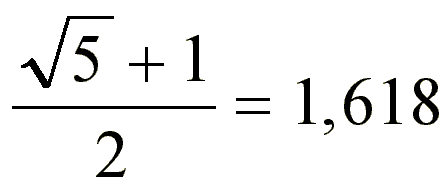
Altın Oran Formülü

Orta Çağ’ın en ünlü matematikçisi olan İtalyan kökenli Leonardo Fibonacci, birbiri arasında ardışık ilişki ve olağanüstü bir oran bulunduğunu iddia ettiği sayıları keşfetmiş ya da diğer bir görüşe göre de Hint-Arap medeniyetinden öğrenmiş ve Avrupa’ya taşımıştır. Evrendeki muhteşem düzenle birebir örtüşen bu sayıları keşfetmesi nedeniyle, altın orana da adının ilk iki harfi olan “Fi” (Φ) sayısı denilmiştir.

Altın Oran, pi (π) gibi irrasyonel bir sayıdır. Ondalık sistemde yazılışı; 1.618033988749894… dür.

Matematik biliminde altın oran sayısı irrasyonel bir sayı olarak kabul edilir ve ve ondalık sistemde yazılışı; 1,618033988749894…’tür. “Fi” şeklinde okunan “Φ” sembolü ile gösterilir. Bu oranın kısaca gösterimi:

olur.

Altın Oranın ifade edilmesi için kullanılan sembol, PHI yani Φ’dir. Altın oranın ondalık gösterimindeki ilk 1557 basamağı:

1.618033988749894848204586834365638117720309179805762862135448622 70526046281890244970720720418939113748475408807538689175212663386

İnsan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. İşte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. İşte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı bize altın oranı verecektir.

Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.

İnsan Vücudu: İnsan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölü- münün alt bölüme oranı altın oranı verceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.

Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. İşte size alaka… Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.

Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır. Ve resimlerinde bu oranı kullanmıştır.

Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz kabuklarına dikkat edenimiz, belki de kolleksiyon yapanımız vardır. İşte deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.

Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş oolduğu tabloları inceleyelim. Mona Lisa: Bu tablonun boyunun enine oranı altın oranı verir. Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.

Elektrik Devresi: Ya demek ki Altın Oran sadece Matematik ve kainatta değil, Fizik’te de kullanılıyormuş. Nasıl mı? Şöyle… Verilen n tane dirençten maximum verim elde etmek için bir paralel bağlama yapılması gerekir. Bu durumda Eşdeğer Direnç, yani Reş= yani altın oran olur.

Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur (-ki biz bu dikdörtgene altın dikdörtgen diyoruz.-) İşte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.

Otomotiv Sanayisinde: Yeni modern arabalarda ki eğim hatlar ve estetik görünümün eğrilik açısı vardır bu altın oran hesabıyla yapılmaktadır.

Kaynaklar

https://www.tech-worm.com/altin-oran-nedir-nerelerde-kullanilir/

https://www.tech-worm.com/fibonacci-dizisi-nedir-nerelerde-kullanilir/https://www.muhendisbeyinler.net/fibonacci-serisi-ve-altin-oran/

https://www.matematikciler.com/fibonacci-dizisi/